DATA SCIENCE, HUMANELY

Carlos Scheidegger, HDC Lab
Department of Computer Science, University of Arizona
NYU Tandon, 2019-03-14

Things that keep me up at night

Reinhart-Rogoff

This work was widely cited as a justification for the austerity measures in the EU

Herndon-Ash-Pollin

This is the world we created!

The data science infrastructure we built is not humane

Predictive Policing

Deployed in major cities: Santa Cruz, Los Angeles, etc.

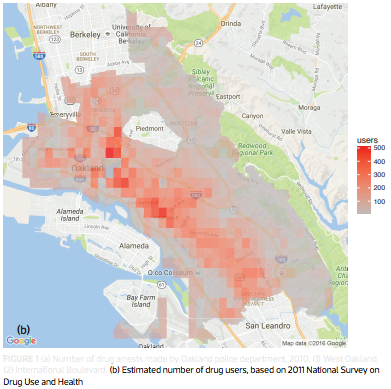
Lum and Isaac, Significance, 2016

This is the world we created!

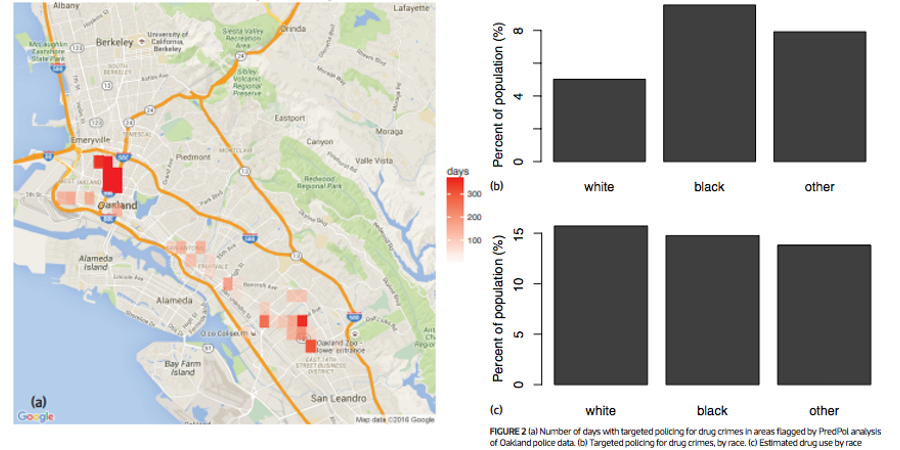
The data science infrastructure we built is inhumane

Our ability to automate has far outpaced our ability to validate

Automation is not going away: we ought to empower people in this new context

DimReader: Axis Lines that Explain Non-Linear Projections

InfoVis 2018

Rebecca Faust, David Glickenstein, Carlos Scheidegger

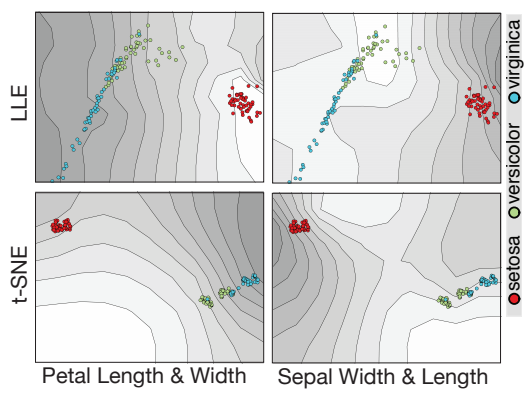
t-SNE plots are beautiful, but what are they showing us?

https://cs.stanford.edu/people/karpathy/cnnembed/cnn_embed_6k.jpg

Shouldn't our tools provide mechanisms for inspecting their own behavior?

A simpler example: the iris dataset

Sepal Length	Sepal Width	Petal Length	Petal Width	Species
5.1	3.5	1.4	0.2	setosa
4.9	3.0	1.4	0.2	setosa
4.7	3.2	1.3	0.2	setosa
...
7.0	3.2	4.7	1.4	versicolor
6.4	3.2	4.5	1.5	versicolor
6.9	3.1	4.9	1.5	versicolor
...
6.3	3.3	6.0	2.5	virginica
5.8	2.7	5.1	1.9	virginica
7.1	3.0	5.9	2.1	virginica
...

t-SNE visualization

Tangent maps of algorithms

author: "User from reddit", CC BY 3.0

Tangent maps of algorithms

First-order understanding: visualizations should inform us about the local context of the data
Influence functions and robust statistics, tools from 1970s: if this point had been more important, how would the model change?
Counterfactual reasoning: "how would Y behave had X been different?". See Google PAIR's What If?

How: Automatic Differentiation ("autodiff")

Differentials are context-free, so rules are syntactic and local
Typical program evaluation: given expression and values of containing variables, you can deduce the value of the expression
With autodiff: given expression, values of containing variables, and values of their derivatives, you can deduce the value of the expression, and the value of its derivatives

Using the tangent map

Option 1: provide a perturbation

This is the mode I've shown you so far
User picks a direction that makes intuitive sense, DimReader measures the direction of change in the projected points, and reconstructs the axis

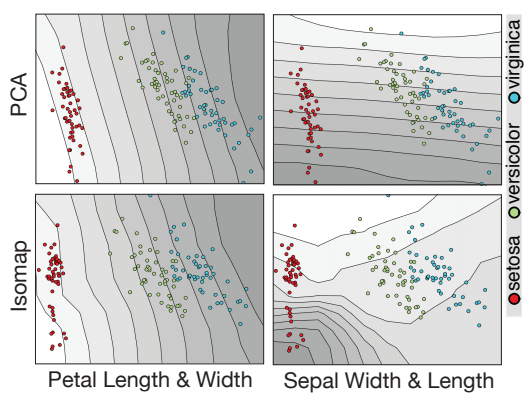
This lets us compare DR methods

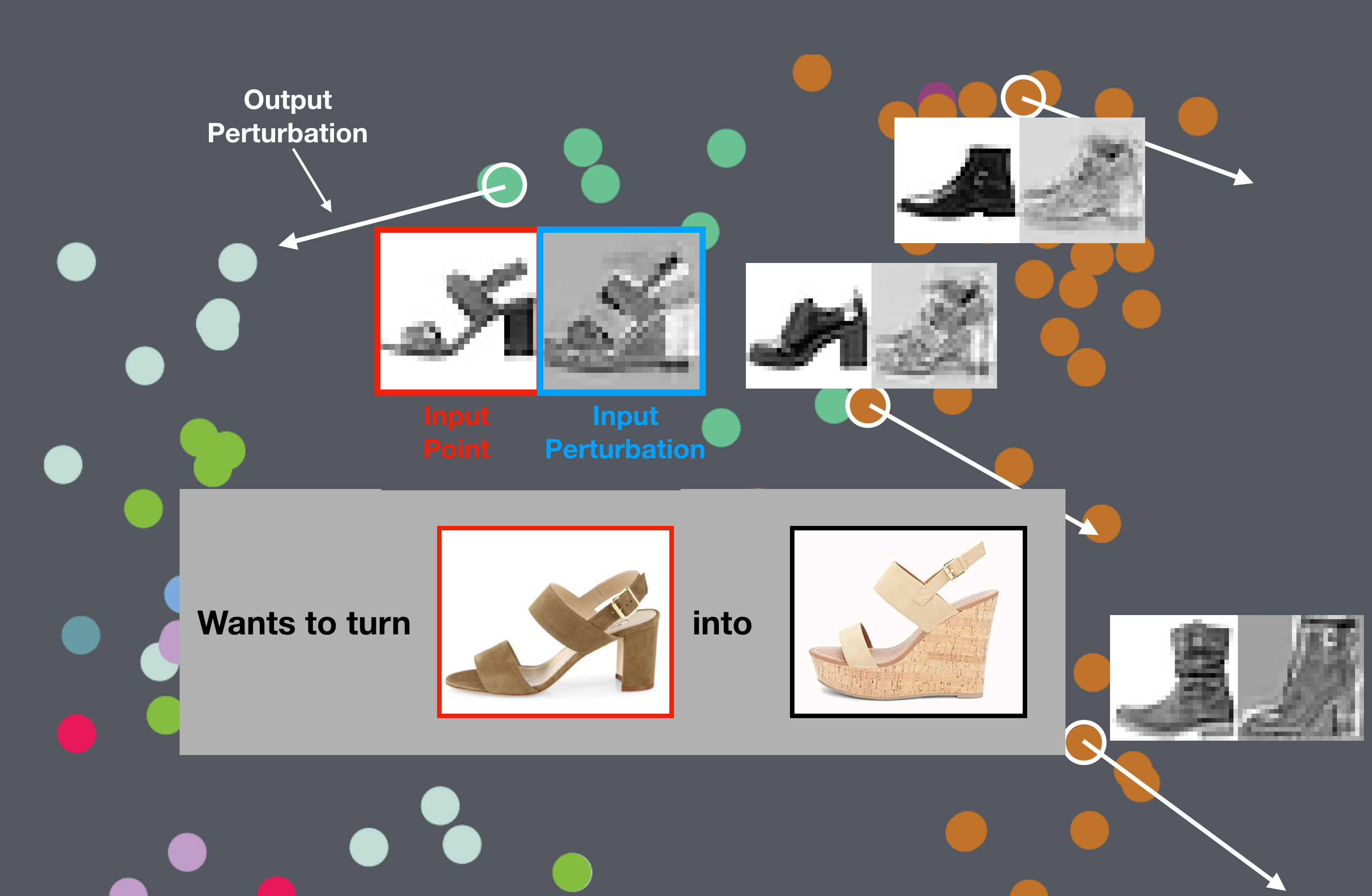
But what if there's no obvious direction?

Option 2: let DimReader infer a good perturbation
We have access to the entire tangent map, let's do math on it

The structure of the tangent map for DR problems

The tangent map is (effectively) sparse and block-structured.
$$\left ( \begin{array}{cccc} B_1 & 0 & \cdots & 0 \\ 0 & B_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & B_n \end{array} \right ) $$
If the DR method sends points from $R^k$ to $R^d$, then each block $B_i$ is $d \times k$

Eigenproblems for Perturbation Discovery

The tangent map is linear, and we will be seeking perturbation directions that maximize some criterion
We focus on the following formulation:
$$\textrm{argmax}_{p \in R^{d \times n}} \sum_i || B_i p_i ||^2 - \lambda \sum_i \sum_j ||p_i - p_j||^2 S(i,j)$$
$$\textrm{s.t.}\ ||p||^2 - 1 = 0$$

Eigenproblems for Perturbation Discovery

$$\textrm{argmax}_{p \in R^{d \times n}} \sum_i || B_i p_i ||^2 - \lambda \sum_i \sum_j ||p_i - p_j||^2 S(i,j)$$
$$\textrm{s.t.}\ ||p||^2 - 1 = 0$$
$B_i$ holds the blocks of the tangent map
$S$ encodes similarity between projection positions
$\lambda$ is a user-specified tradeoff parameter

Results: t-SNE projection on MNIST-Fashion

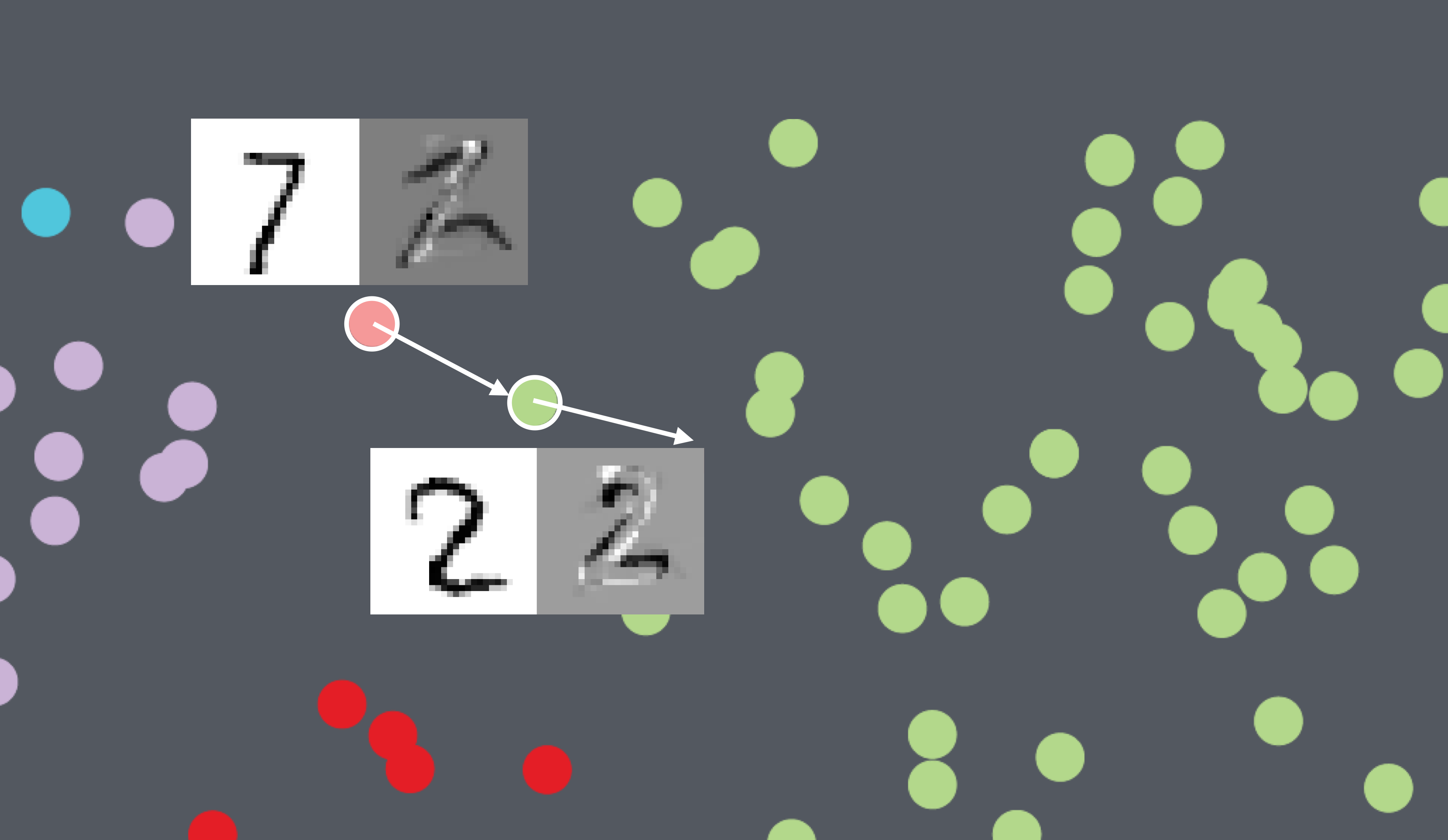
Results: t-SNE projection on MNIST-Digits

Results: t-SNE projection on Iris dataset

Outlook

Can we design novel DR methods that yield good DimReader plots?
What other visualization methods would benefit from first-order information?

Runaway Feedback Loops in Predictive Policing

FAT* 2018

Danielle Ensign, Sorelle Friedler, Scott Neville, Carlos Scheidegger, Suresh Venkatasubramanian

Predictive Policing

Previous Work

Lum and Isaac, 2016: What happens when predictive policing systems are trained on biased data?

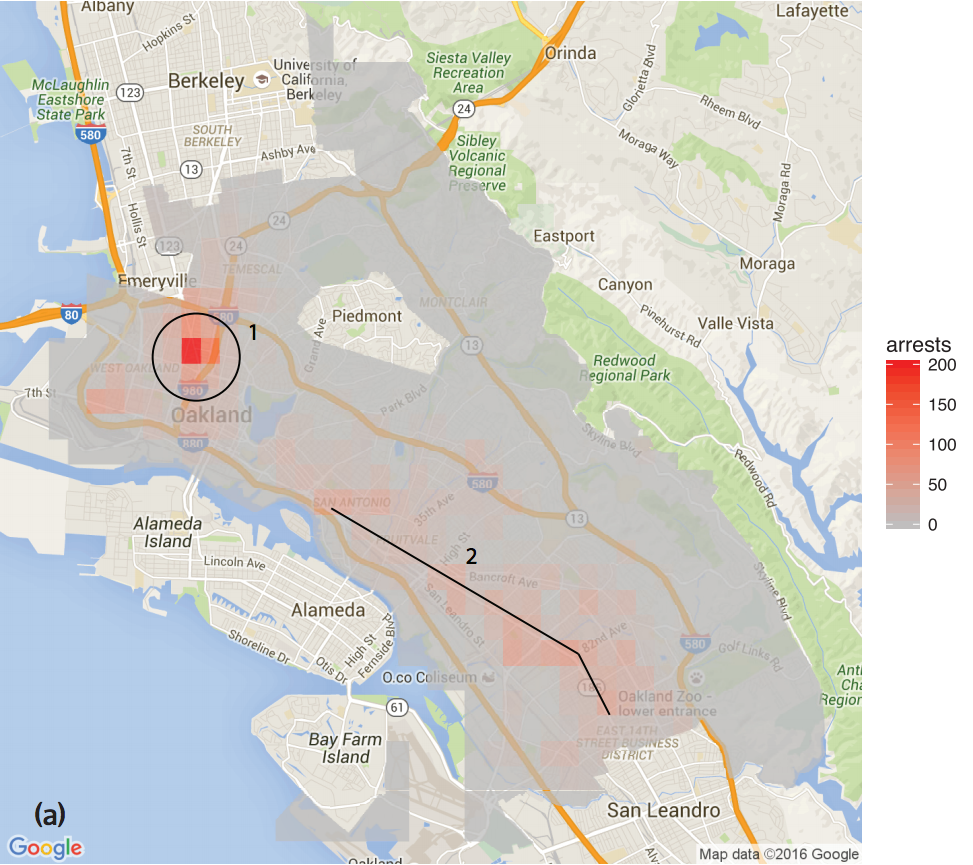
Previous Work

Lum and Isaac, 2016: What happens when predictive policing systems are trained on biased data?

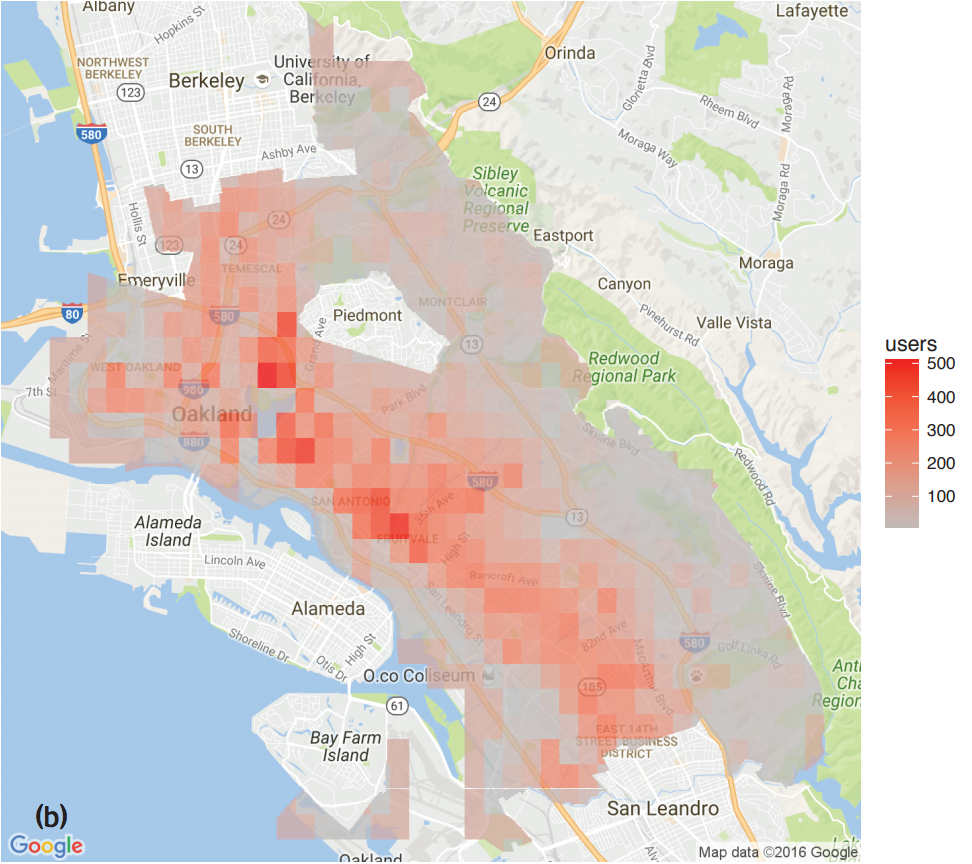
Does targeted predictive policing cause feedback?

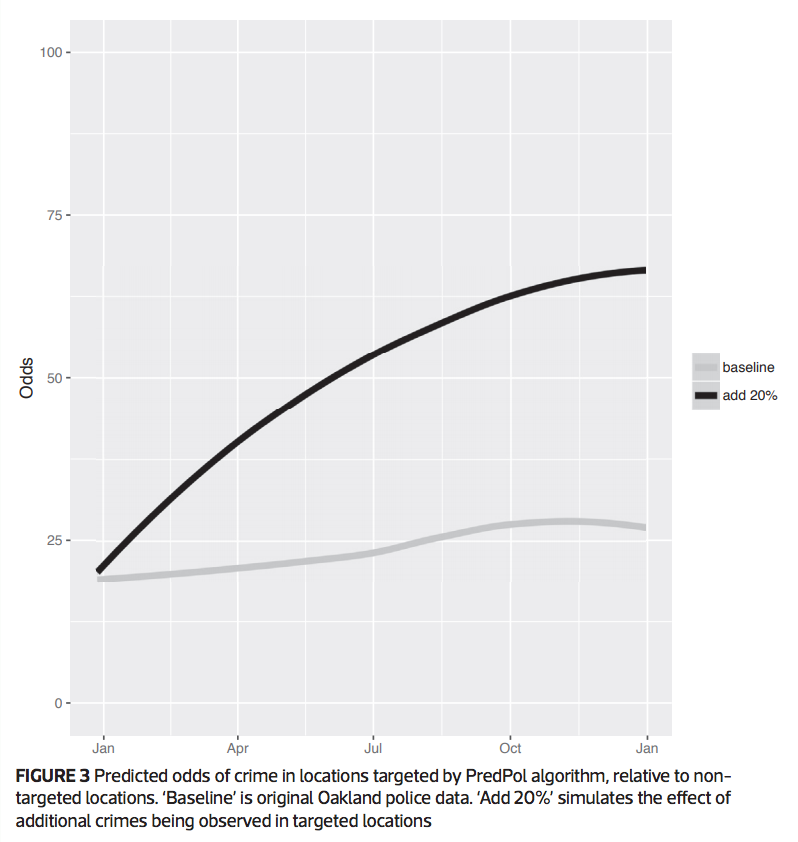
Our contributions

A simple model in which such feedback loops happen: Pólya-Eggenberger urns
A mitigation mechanism that solves the problem in the simplified model
Experimental evidence that this feedback loop explains Lum and Isaac's observations

Goals, Assumptions

Goal: Effective policing - A region with fraction $\alpha$ of the crime should receive $\alpha$ of the policing effort
Assumption: Predictive Model - Policing happens by visiting regions proportionally to probability estimated by model
Assumption: Limited context - we only store crime counts
Assumption: Truth in data - Policing uncovers crime exactly at the rate of crime occurrence

Pólya-Eggenberger Urns

Start with an urn containing $r$ and $b$ red and black balls
Repeat:
- Draw a ball at random from urn, note its color
- If color was red, add $rr$ red balls, and $rb$ black balls. if black, add $br$ red balls, and $bb$ black balls.
- $$\left ( \begin{array}{cc} rr & rb \\ br & bb \end{array} \right )$$

Pólya-Eggenberger Urns

Pólya-Eggenberger Urns are reasonable models for predictive policing
Different colors correspond to different regions
As more crime happens in one area, we should direct more effort to that area

The simple case: Pólya Urn

Consider the following update matrix: $\left ( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right )$
Let's run this process 50 times

The simple case: Pólya Urn

Consider the following update matrix: $\left ( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right )$
Let's run this process 10,000 times

What about $\left ( \begin{array}{cc} 2 & 0 \\ 0 & 1 \end{array} \right )$ ?

What about $\left ( \begin{array}{cc} 2 & 0 \\ 0 & 1 \end{array} \right )$ ?

What's going wrong?

As police record more crime in a region, they're more likely to go there
- This makes sense
But as police is more likely to go to a region, they're also more likely to see crime there!
- This is the crux of the problem

Intuition

If we often police $a$, then we already expect crime at $a$, and shouldn't (relatively) be surprised to see crime at $a$
If we're twice as likely to go to $a$ than $b$, then we should be half as willing to count our observations there
With this modified urn, the ratio of balls will always converge to the ratio of the diagonal values
- And hence, no feedback loops

Two explanations

If we think of policing as "surveying crime", then our mitigation strategy is exactly the Thompson-Horvitz estimator for unequal-probability survey sampling
If we think of the decision of where to go as tossing a biased coin, then our mitigation strategy for recording unbiased observations is exactly Von Neumann's classic trick for getting unbiased tosses from biased coins

What about $\left ( \begin{array}{cc} 2 & 0 \\ 0 & 1 \end{array} \right )$ ?

What about $\left ( \begin{array}{cc} 2 & 0 \\ 0 & 1 \end{array} \right )$ ?

But does this actually explain Isaac and Lum's results?

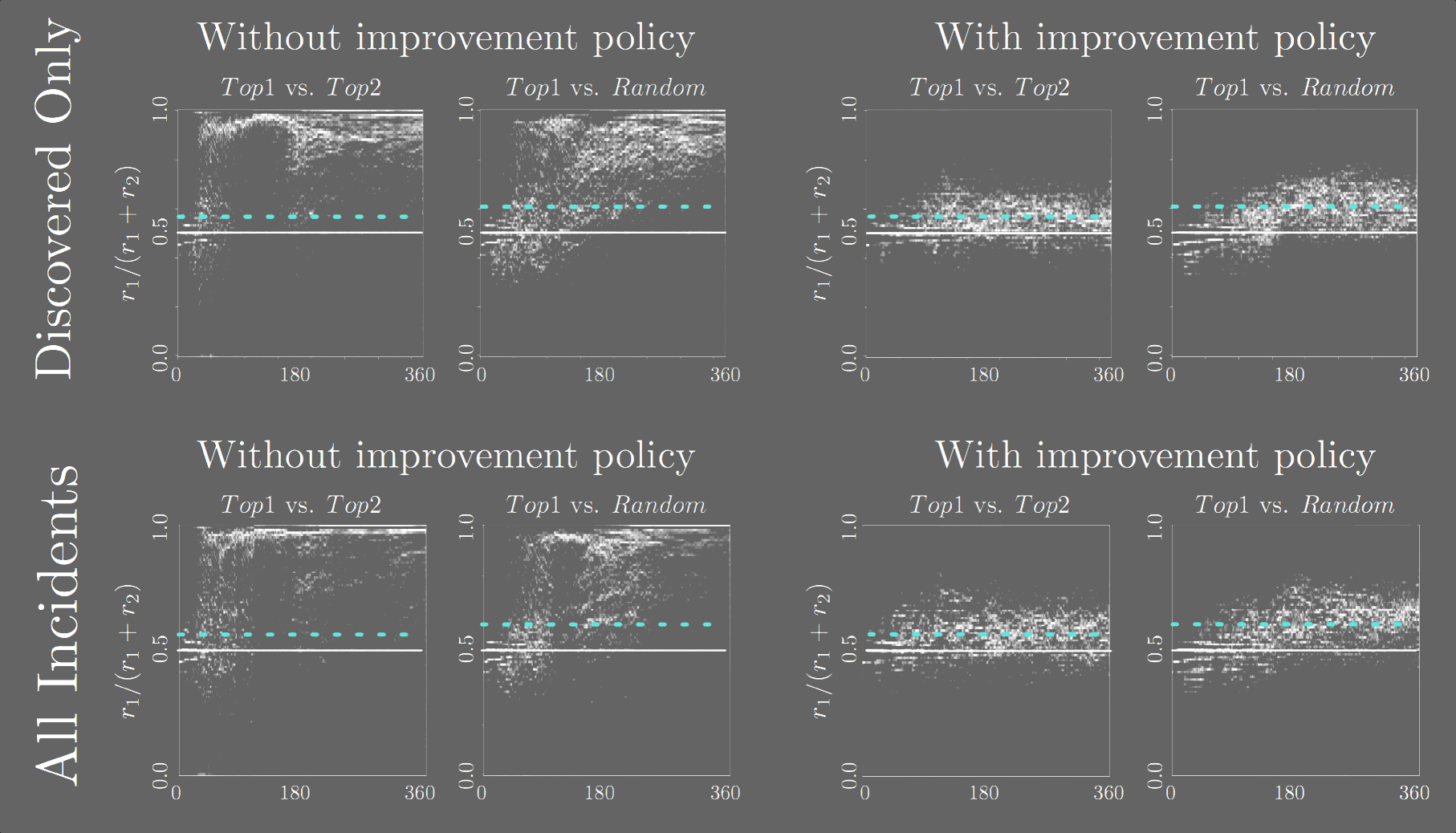
Limitations, Caveats

Our findings are not unassailable evidence that PredPol is broken
More importantly, our mitigation strategy is not evidence that "now PredPol is fixed"
We think of it as a serious threat to validity and an explanation mechanism, not as a bugfix
We also think that batch learning is fundamentally broken in this setting (see our followup ALT paper for a bandit approach)

Acknowledgments

Without William Isaac and Kristian Lum's willingness to help and share their results, this would have been literally impossible to write

Where to now?

We build inhumane systems at our peril
Worse yet, we build inhumane systems at the peril of those powerless to contest the system's decisions
We can choose to build a better world

Thank you!

https://cscheid.net

https://hdc.cs.arizona.edu

cscheid@cs.arizona.edu