[title: line-fit] Shapley, Grad, Fourier, and All That

What is this talk

• A chapter in the story of us trying to make sense of “explanations” in “explainable AI”

• tl;dr: they don’t explain much and what they do explain, they do it strangely

• Calculations ahead! Everyone ready? 3, 2, 1…

Shapley What?

• Alice and Bob own a left-hand glove; Claire owns a right-hand glove. A pair is worth 1 dollar, but either hand by itself is worth nothing.

  • How much should you offer each player to participate in the game?

• Shapley Values assign credit to players

SV: two classic definitions

• $ \varphi_i(v) = \sum_{S \subset N \backslash \{i\} } \frac{|S|! (n - |S| - 1)!}{n} \left ( v(S \cup \{i\} ) - v(S) \right ) $

  • Weighted average marginal contribution over coalitions

• Only functional that satisfies linearity, symmetry, and “efficiency”

  • Efficiency means “sum of shapley values equal value of the game for the full set of players”

Shapley Values and ML Explanations

• Widely used in ML for feature importance explanations: “how important is gender for this health risk classifier?”

• Define a game with one feature per player, define feature importance as the Shapley Value of player.

• We think this is problematic on many grounds; today, we give a purely mathematical critique.

Some examples

1. $(0, 0, 0, 2)$: “everyone is needed”
2. $(0, 1, 1, 2)$: “ships passing in the night”
3. $(0, 10, 10, 2)$: “we’re each great but not good together”

• Shapley Values for all of these are the same: $(1, 1)$
• “Inessential games” are games where “players don’t interact” (example 2).

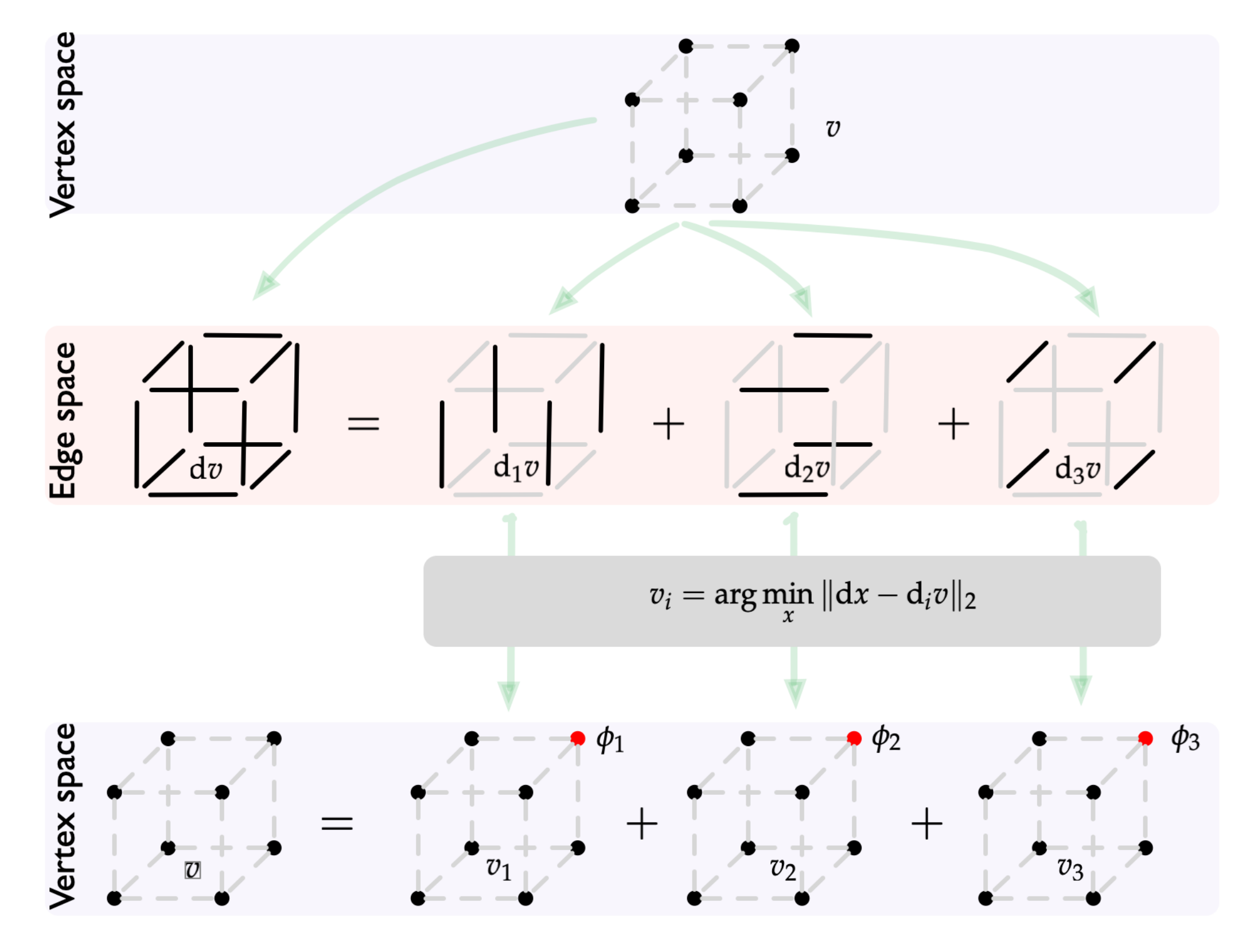
[title: line-fit] (S&T, 2017): Shapley from Gradients

Take the game on a hypercube, and define the gradient $\nabla$. Decompose $\nabla$ in $\nabla_1, \dots, \nabla_d$ such that $\sum_i \nabla_i = \nabla$.

Fourier Transforms

• The FT on a hypercube converts between a representation of function on sets and a multilinear polynomial
  • “set” basis: weights are values of the game for each coalition
  • “polynomial” basis: weights are the coefficients for each multilinear monomial
• Takeaway 1: a game is inessential iff its corresponding polynomial is strictly linear

Fourier Transforms

• \[{\small \begin{array}{cc} \begin{array}{ccc}\textrm{set}&\textrm{position}&\textrm{value} \\ \hline \{\} & (1, 1) & 0 \\ \{1\} & (-1, 1) & 1 \\ \{2\} & (1, -1) & 1 \\ \{1,2\} & (-1, -1) & 0 \end{array} & \begin{array}{cc}\textrm{monomial}&\textrm{coefficient} \\ \hline 1 & 1/2 \\ p_1 & -1/4 \\ p_2 & -1/4 \\ p_1p_2 & 1/2 \end{array} \end{array}}\]
• In set basis, $(0, 1, 1, 0)$
• $f(p_1, p_2) = 1/2 - (1/4) p_1 - (1/4) p_2 + (1/2) p_1 p_2$
• In polynomial basis, $(1/2, -1/4, -1/4, 1/2)$

Fourier Transforms

• \[{\small \begin{array}{cc} \begin{array}{ccc}\textrm{set}&\textrm{position}&\textrm{value} \\ \hline \{\} & (1, 1) & 0 \\ \{1\} & (-1, 1) & 1 \\ \{2\} & (1, -1) & 1 \\ \{1,2\} & (-1, -1) & 2 \end{array} & \begin{array}{cc}\textrm{monomial}&\textrm{coefficient} \\ \hline 1 & 1/2 \\ p_1 & -1/4 \\ p_2 & -1/4 \\ p_1p_2 & 0 \end{array} \end{array}}\]
• In set basis, $(0, 1, 1, 2)$
• $f(p_1, p_2) = 1/2 - (1/4) p_1 - (1/4) p_2$
• In polynomial basis, $(1/2, -1/4, -1/4, 0)$

Now we analyze $\nabla^\dagger \nabla_i$

• \[\begin{eqnarray*} v_i &=& \textrm{argmin}_u ||\nabla u - \nabla_i v || \\ &=& \nabla^\dagger \nabla_i v \\ &=& (\nabla^* \nabla)^\dagger (\nabla^* \nabla_i) v \\ &=& L^\dagger (\nabla^* \nabla_i) v \end{eqnarray*}\]

• $L$ is the Laplacian operator, and its eigenvectors are the Fourier Transform matrix.

• They are also eigenvectors of $\nabla^* \nabla_i$, letting us push the gradient definition of SVs into the FTs

Our result: a novel formula for SVs based on FTs

• Closed-form formula for Shapley Values from polynomial basis coefficients

• Shapley value for a player equals $-2 \times k$, where $k$ is the sum of all odd-degree coefficients of monomials containing that player, each divided by the degree of the monomial.

[title: line-fit] Examples, tying back to ML explanations

• For 2-feature model with polynomial $c_1 1 + c_a a + c_b b + c_{ab} a b$, the Shapley value for player $a$ is $-2c_a$ (seems fine, but where’s $c_{ab}$?)

• For 3-feature model: $-2(c_a + c_{abc}/3)$ (hmm…)

• For 4-feature model: $-2(c_a + c_{abc}/3 + c_{abd}/3 + c_{acd}/3)$ (uh…)

• For 5-feature model: 1 linear term, 6 cubic terms, 1 quintic term (????)

• Shapley Values are weird: there’s no good reason that expression is a good summary of the feature importances.

Thank you!

• Takeaways:

  1. A game is inessential iff its corresponding polynomial is strictly linear. Polynomials seem to be good explanations for feature importance games!

  2. There’s a deep connection between SVs and FTs via $\nabla$ and its SVD

  3. SVs are very weird objects for ML feature importance explanations. Be skeptical of interpretation methods using them.

• Questions? (We’re still working on the writeup…)

References

1. Problems with Shapley Values… Kumar et al, ICML 2019, arXiv:2002.11097
2. Hodge decomposition and the Shapley value of a cooperative game. Stern & Tettenhorst, Games & Econ. Behav. arXiv:1709.08318

Extras

Speculation

• Where does the problem arise?

• Our opinion: the axiom of efficiency makes sense in the context of cooperative games, but is pretty silly in feature importance explanations. We don’t want signed values to sum up to the total contribution: we want magnitudes.

• We think orthogonality is a much better choice, and leads to a much simpler “explanation”: the FT representation itself!

[title: line-fit] Grad: Shapley Values from Gradients

• Define one subgame per player

  \[\begin{eqnarray*}v_i &=& \textrm{argmin}_{u} || \nabla u - \nabla_i v ||_2 \\ \varphi_i(v) &=& v_i[U] - v_i[\emptyset]\end{eqnarray*}\]

$\varphi_i(v) = v_i[U] - v_i[\emptyset]$: proof

• \[\begin{eqnarray*}v_i &=& \nabla^\dagger \nabla_i v\\ \sum_i v_i &=& \nabla^\dagger \sum_i \nabla_i v \\ &=& \nabla^\dagger \nabla v\end{eqnarray*}\]

• $\nabla^\dagger \nabla_i$ is a linear operator, and $\sum_i v_i[U] - v_i[\emptyset] = v[U] - v[\emptyset]$.

• $v \mapsto (v_1[U] - v_1[\emptyset], \ldots, v_d[U] - v_d[\emptyset])$ is linear, symmetric, and efficient, hence these are the Shapley Values.

The Calculation (1/3)

• \[\begin{eqnarray*} & L^\dagger \nabla^* \nabla_i & \\ & = & 2^N F \textrm{diag}(s \mapsto (2|s|)^{-1}) F 2^N F \textrm{diag}(s \mapsto 2[i \in s]) F \\ & = & 2^N F \textrm{diag}(s \mapsto (2|s|)^{-1}) \textrm{diag}(s \mapsto 2[i \in s]) F \\ & = & 2^N F \textrm{diag}(s \mapsto [i \in s]|s|^{-1}) F \end{eqnarray*}\]

The Calculation (2/3)

• \[\begin{eqnarray*} \varphi(v, i) & = & v_i(N) - v_i(\emptyset) \\ & = & (-1, 0, \cdots, 0, 1)^T v_i \\ & = & (-1, 0, \cdots, 0, 1)^T 2^N F \textrm{diag}(s \mapsto [i \in s] (|s|)^{-1}) F v \end{eqnarray*}\]

The Calculation (3/3)

• \[F (-1, 0, \cdots, 0, 1) = \\ -2^N \times -2(x_1 + x_2 + \cdots + x_n + x_1x_2x_3 + x_1x_2x_4 + \cdots)\]